
The only nonzero singular value is the product of the normalizing factors.

These vectors provide bases for the one dimensional column and row spaces. The first left and right singular vectors are our starting vectors, normalized to have unit length. The matrix $A$ is their outer product A = u*v' Here is an example involving lines in two dimensions. So the columns of $V$, which are known as the right singular vectors, form a natural basis for the first two fundamental spaces. This says that $A$ maps the first $r$ columns of $V$ onto nonzero vectors and maps the remaining columns of $V$ onto zero. Write out this equation column by column. The only nonzero elements of $\Sigma$, the singular values, are the blue dots.

I've drawn a green line after column $r$ to show the rank. Multiply both sides of $A = U\Sigma V^T $ on the right by $V$. So the function r = rank(A)Ĭounts the number of singular values larger than a tolerance. With inexact floating point computation, it is appropriate to take the rank to be the number of nonnegligible diagonal elements. In MATLAB, the SVD is computed by the statement. The signs and the ordering of the columns in $U$ and $V$ can always be taken so that the singular values are nonnegative and arranged in decreasing order.įor any diagonal matrix like $\Sigma$, it is clear that the rank, which is the number of independent rows or columns, is just the number of nonzero diagonal elements. All of the other elements of $\Sigma$ are zero. The diagonal elements of $\Sigma$ are the singular values, shown as blue dots. Here is a picture of this equation when $A$ is tall and skinny, so $m > n$. The matrix $A$ is rectangular, say with $m$ rows and $n$ columns $U$ is square, with the same number of rows as $A$ $V$ is also square, with the same number of columns as $A$ and $\Sigma$ is the same size as $A$. The shape and size of these matrices are important. The matrix $\Sigma$ is diagonal, so its only nonzero elements are on the main diagonal.
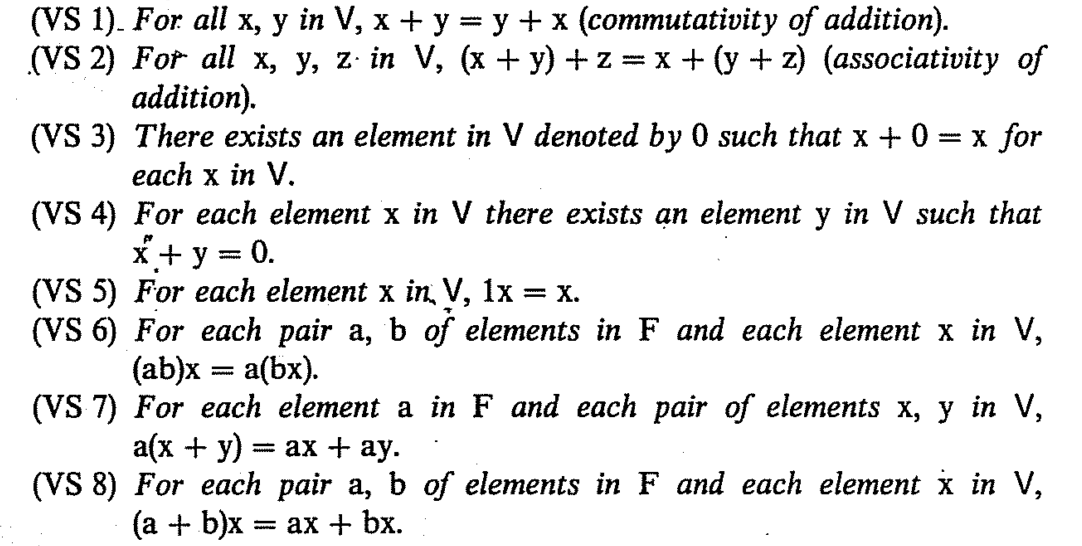
The matrices $U$ and $V$ are orthogonal, which you can think of as multidimensional generalizations of two dimensional rotations. The natural bases for the four fundamental subspaces are provided by the SVD, the Singular Value Decomposition, of $A$. The rank of a matrix is this number of linearly independent rows or columns. This may seem obvious, but it is actually a subtle fact that requires proof. In other words, the number of linearly independent rows is equal to the number of linearly independent columns. The dimension of the row space is equal to the dimension of the column space.If the answer to both of these questions is yes, then \(U\) is a vector space. If we multiply any vector in \(U\) by any constant, do we end up with a vector in \(U\)?.If we add any two vectors in \(U\), do we end up with a vector in \(U\)?.

That is, if we have some set \(U\) of vectors that come from some bigger vector space \(V\), to check if \(U\) itself forms a smaller vector space we need check only two things: We can use this theorem to check if a set is a vector space. Note that the requirements of the subspace theorem are often referred to as "closure''. All of the other eight properties is true in \(U\) because it is true in \(V\). We know that the additive closure and multiplicative closure properties are satisfied. That is, we need to show that the ten properties of vector spaces are satisfied. \( \newcommand\) in \(U\) and all constants \(\mu, \nu\), then \(U\) is a vector space.


 0 kommentar(er)
0 kommentar(er)
